The observation that traffic in packet-switched networks shows self-similar and long-range dependent behaviour goes back to local area Ethernet investigations made by Willinger et al. [4]. In the sequel, a lot of empiric studies have been made that confirm the self-similar nature of packet-switched traffic in local and wide area networks and for different kinds of applications [5]. While exact or asymptotic self-similarity does not always exactly fit to observed empiric traffic samples, it still comes closer to empiric observations than Poisson-based traffic models do. In particular, the effects of burstiness at different time scales and long-range dependence (see below) cannot be modelled by Poisson traffic models.
Mathematically speaking, let ![]() be the number of packets traversing a link during the
time interval
be the number of packets traversing a link during the
time interval ![]() Then the properties of the sequence
Then the properties of the sequence ![]() with
with
are investigated. ![]() and
and ![]() are assumed to be realizations of stationary stochastic
processes
are assumed to be realizations of stationary stochastic
processes ![]() and
and ![]() respectively. In the following, the description of the
properties of self-similar time series will concentrate on the theoretical
values
respectively. In the following, the description of the
properties of self-similar time series will concentrate on the theoretical
values ![]() and
and ![]() It should be clear,
that the empirically observed number of packets must be interpreted as
realizations of these stochastic processes.
It should be clear,
that the empirically observed number of packets must be interpreted as
realizations of these stochastic processes.
For the analysis of the properties of the time series ![]() it makes sense to introduce the scaled sample
it makes sense to introduce the scaled sample
![$\displaystyle X^{(m)}_k := \frac{1}{m} \left[ X_{(k-1)m + 1} + \cdots + X_{km} \right], $](main-Dateien/img11.png)
the scaled variance
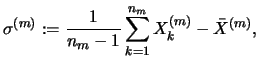
where ![]() denotes the number of scaled samples (it is assumed that
denotes the number of scaled samples (it is assumed that ![]() ) and
) and ![]() denotes the mean
denotes the mean
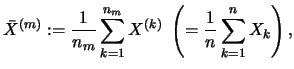
and the autocorrelation functions
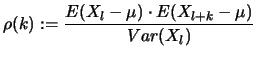
and
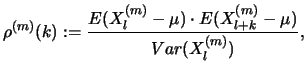
respectively.
The following definition is taken from [7].
Definition: The time series ![]() is called asymptotically second order self-similar
with self-similarity parameter or Hurst parameter
is called asymptotically second order self-similar
with self-similarity parameter or Hurst parameter ![]() if the
second-order statistics of
if the
second-order statistics of ![]() converge as
follows:
converge as
follows:
If equities (1)
and (2)
are valid for all ![]() and not only for the limit, the time series is said to be exactly
self-similar of second order.
and not only for the limit, the time series is said to be exactly
self-similar of second order. ![]()
For the modeling of traffic in packet-switched networks, only the range ![]() is relevant. With
the presented mathematical framework, the main properties of self-similar time
series with
is relevant. With
the presented mathematical framework, the main properties of self-similar time
series with ![]() within this range can be expressed as follows [1]
within this range can be expressed as follows [1]
There are a variety of methods for the generation of self-similar and long-range dependent traffic for simulation experiments: